PRUEBA DE HIPÓTESIS

La prueba de hipótesis suele comenzar con alguna teoría, afirmación, o aseveración sobre un parámetro especifico de una población. Por ejemplo, su hipótesis inicial sobre el ejercicio del cereal es que el proceso está funcionando adecuadamente, lo que significa que el promedio de llenado es de 368 gramos, y que no es necesario emprender acciones correctivas. La hipótesis de que el parámetro poblacional es igual a la especificación de la empresa denomina hipótesis nula. Una hipótesis nula siempre es una de status quo, y se denota mediante el símbolo.

Hipótesis nula (H0)

La hipótesis nula indica que un parámetro de población (tal como la media, la desviación estándar, etc.) es igual a un valor hipotético. La hipótesis nula suele ser una afirmación inicial que se basa en análisis previos o en conocimiento especializado.

Hipótesis alternativa (H1)

La hipótesis alternativa indica que un parámetro de población es más pequeño, más grande o diferente del valor hipotético de la hipótesis nula. La hipótesis alternativa es lo que usted podría pensar que es cierto o espera probar que es cierto.

Con base en los datos de muestra, la prueba determina si se puede rechazar la hipótesis nula. Usted utiliza el valor p para tomar esa decisión. Si el valor p es menor que el nivel de significante (denotado como α o alfa), entonces puede rechazar la hipótesis nula.

Un error común de percepción es que las pruebas estadísticas de hipótesis están diseñadas para seleccionar la más probable de dos hipótesis. Sin embargo, al diseñar una prueba de hipótesis, establecemos la hipótesis nula como lo que queremos desaprobar. Puesto que establecemos el nivel de significancia para que sea pequeño antes del análisis (por lo general, un valor de 0.05 funciona adecuadamente), cuando rechazamos la hipótesis nula, tenemos prueba estadística de que la alternativa es verdadera. En cambio, si no podemos rechazar la hipótesis nula, no tenemos prueba estadística de que la hipótesis nula sea verdadera. Esto se debe a que no establecimos la probabilidad de aceptar equivocadamente la hipótesis nula para que fuera pequeña.

Ejercicios resueltos de prueba de hipótesis

1) Una empresa está interesada en lanzar un nuevo producto al mercado. Tras realizar una campaña publicitaria, se toma la muestra de 1 000 habitantes, de los cuales, 25 no conocían el producto. A un nivel de significación del 1% ¿apoya el estudio las siguientes hipótesis?

• a. Más del 3% de la población no conoce el nuevo producto.
• b. Menos del 2% de la población no conoce el nuevo producto

Datos:

n = 1000

x = 25

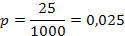
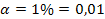
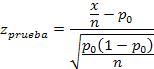
Donde:

x = ocurrencias

n = observaciones

= proporción de la muestra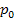

= proporción propuesta

Solución:

a)

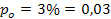
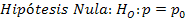
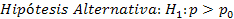
a = 0,01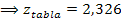 

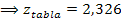
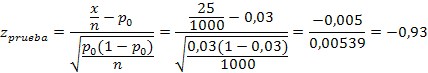
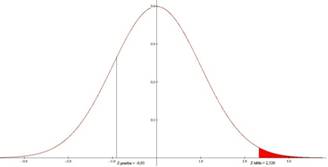
H0 es aceptada, ya que zprueba (-0,93) es menor que ztabla (2,326), por lo que no es cierto que más del 3% de la población no conoce el nuevo producto.

En Excel

b)

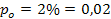
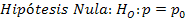
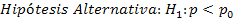
a = 0,01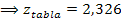 

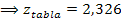
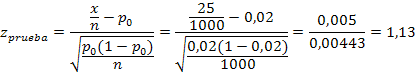
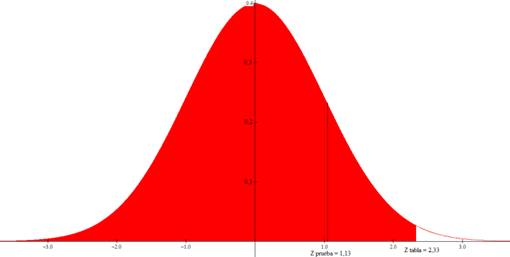
H0 es rechazada, ya que zprueba (1,13) es menor que ztabla (2,326), por lo que es cierto que menos del 2% de la población no conoce el nuevo producto.

2) Cuando las ventas medias, por establecimiento autorizado, de una marca de relojes caen por debajo de las 170,000 unidades mensuales, se considera razón suficiente para lanzar una campaña publicitaria que active las ventas de esta marca. Para conocer la evolución de las ventas, el departamento de marketing realiza una encuesta a 51 establecimientos autorizados, seleccionados aleatoriamente, que facilitan la cifra de ventas del último mes en relojes de esta marca. A partir de estas cifras se obtienen los siguientes resultados: media = 169.411,8 unidades., desviación estándar = 32.827,5 unidades. Suponiendo que las ventas mensuales por establecimiento se distribuyen normalmente; con un nivel de significación del 5 % y en vista a la situación reflejada en los datos. ¿Se considerará oportuno lanzar una nueva campaña publicitaria?

Datos:

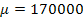
n = 51

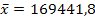
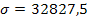
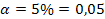
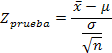
Solución:

H0: ( = 170000

H1: ( < 170000

a = 0,05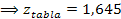 

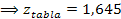
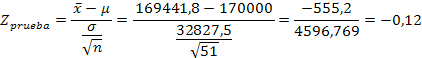
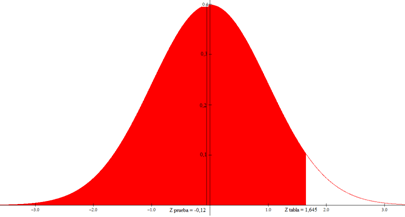
Se rechaza Ho, porque zprueba (-0,12) es menor que ztabla (1,645), por lo tanto se acepta H1: ( < 170000, y se debe considerar oportuno lanzar una nueva campaña publicitaria.

En Excel

Ejercicio propuesto :

3) Un gerente de ventas de libros universitarios afirma que en promedio sus representantes de ventas realiza 40 visitas a profesores por semana. Varios de estos representantes piensan que realizan un número de visitas promedio superior a 40. Una muestra tomada al azar durante 8 semanas reveló un promedio de 42 visitas semanales y una desviación estándar de 2 visitas. Utilice un nivel de confianza del 99% para aclarar esta cuestión.