Tabla de la distribución normal
La tabla de la distribución normal presenta los valores de probabilidad para una variable estándar Z, con media igual a 0 y varianza igual a 1.
Para usar la tabla, siempre debemos estandarizar la variable por medio de la expresión:
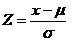
Siendo el valor de interés; la media de nuestra variable y su desviación estándar. Recordemos que y corresponden a parámetros, o sea valores en el universo, que generalmente no conocemos, por lo que debemos calcular Z usando los datos de nuestra muestra.
En general, el valor de Z se interpreta como el número de desviaciones estándar que están comprendidas entre el promedio y un cierto valor de variable x. En otras palabras, se puede decir que es la diferencia entre un valor de la variable y el promedio, expresada esta diferencia en cantidad de desviaciones estándar.
Suena abstracto, pero con un ejemplo se podrá entender mejor:
Supongamos un conjunto de personas con edad promedio 25 años y desviación estándar 3,86. Nuestro valor de interés (x) es 30 años. El valor de Z correspondiente será:
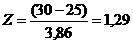
Este valor de Z nos dice que la edad de 30 años está a 1,29 desviaciones estándar sobre el promedio.
Ahora bien, la tabla de la distribución normal, entrega valores de probabilidad para los distintos valores de Z.
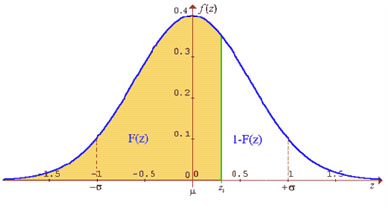
¿Cómo se usa la tabla de Z?
Lo averiguaremos con un valor concreto: ¿cuál es la probabilidad de encontrar un valor de Z menor o igual a 1,96?
Vamos a la tabla y familiaricémonos con algunas de sus características.
▪ En la primera columna de la tabla aparece el entero y primer decimal del valor de Z, vemos que los valores van desde -3,4 a 3,3. En la primera fila (arriba), aparece el segundo decimal del valor de Z y, como es lógico, hay 10 números (0,00 a 0,09).
▪ Entonces, para nuestro valor de Z = 1,96 buscaremos 1,9 en la primera columna de la tabla y 0,06 en la primera fila de la tabla. Trazaremos líneas perpendiculares desde esos valores y llegaremos a un número en el cuerpo de la tabla (véase la tabla más abajo, que tiene marcadas las dos perpendiculares de las que hablamos. El número que encontramos y que está destacado es: 0,9750.
▪ Por lo tanto, la probabilidad asociada a Z=1,96 es 0,9750, es decir, la probabilidad de encontrar un valor de Z menor o igual a 1,96 es 0,9750.
En nuestro ejemplo anterior, con la edad 30 años, vemos que el valor Z = 1,29 tiene una probabilidad asociada de 0,9014. Entonces, la probabilidad de encontrar una persona con edad de 30 años o menos, en este grupo humano, es 0,9014.
Ejercicios
Calcular la proporción de estudiantes que tienen puntuaciones que exceden por lo menos en cinco puntos de la puntuación que marca la frontera entre el Apto y el No-Apto (son declarados No-Aptos el 25% de los estudiantes que obtuvieron las puntuaciones más bajas)
p class="b">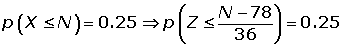
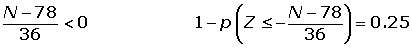
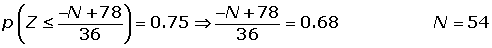
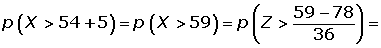
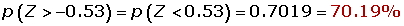
Un estudio ha mostrado que, en un cierto barrio, el 60% de los hogares tienen al menos dos televisores Se elige al azar una muestra de 50 hogares en el citado barrio. Se pide:
1¿Cuál es la probabilidad de que al menos 20 de los citados hogares tengan cuando menos dos televisores?
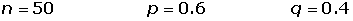

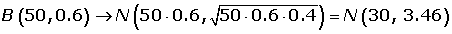
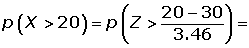
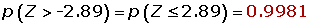 2¿Cuál es la probabilidad de que entre 35 y 40 hogares tengan cuando menos dos televisores?
2¿Cuál es la probabilidad de que entre 35 y 40 hogares tengan cuando menos dos televisores?
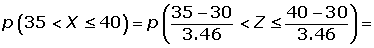
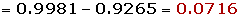
Ejercicio propuesto
En un examen tipo test de 200 preguntas de elección múltiple, cada pregunta tiene una respuesta correcta y una incorrecta. Se aprueba si se contesta a más de 110 respuestas correctas. Suponiendo que se contesta al azar, calcular la probabilidad de aprobar el examen.
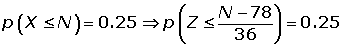
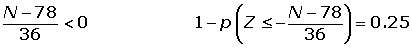
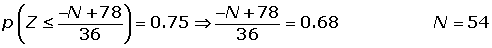
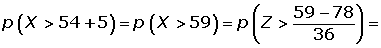
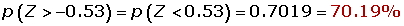
1¿Cuál es la probabilidad de que al menos 20 de los citados hogares tengan cuando menos dos televisores?
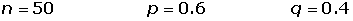

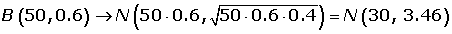
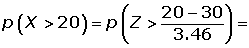
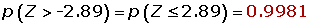
2¿Cuál es la probabilidad de que entre 35 y 40 hogares tengan cuando menos dos televisores?
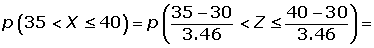
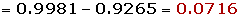
Ejercicio propuesto
En un examen tipo test de 200 preguntas de elección múltiple, cada pregunta tiene una respuesta correcta y una incorrecta. Se aprueba si se contesta a más de 110 respuestas correctas. Suponiendo que se contesta al azar, calcular la probabilidad de aprobar el examen.


No hay comentarios:
Publicar un comentario